
| Home |
| The WEB-Method |
| Examples |
| Publications |
| Contact |
Helmholtz Equation
The group of the physicist Prof. Dr. A. Richter uses experiments with microwaves to study quantum manifestation of classical chaos. To this end, they build super-conductive microwave resonators and measure the spectrum of eigenvalues. For details click here.
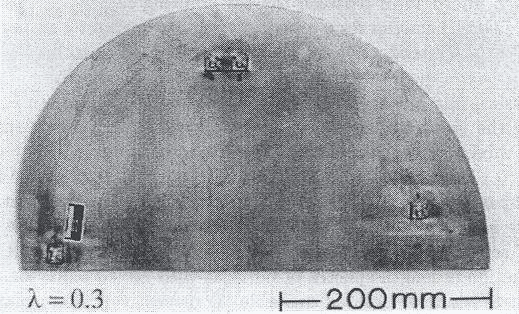
As an example the following picture shows a flat resonator for a Pascalian snail:
The physical experiment is mathematically described by the stationary Helmholtz equation:
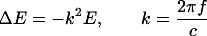
The finite element discretisation of this equation leads to a generalised eigenvalue problem:
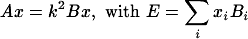
Using Web-Splines of degree 5 on a 75x75 grid we are able to compute 2000 eigenvalues with relative error less then 10-4 in half an hour on a 2 GHz standard PC .
Here are some examples of the corresponding eigenfunctions:
first eigenfunction, k2 = 106.6774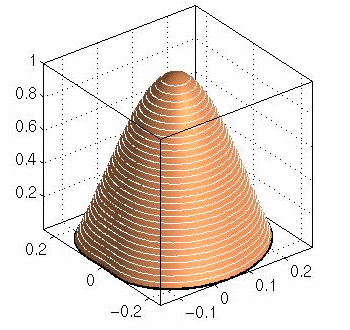
second eigenfunction, k2 = 254.2339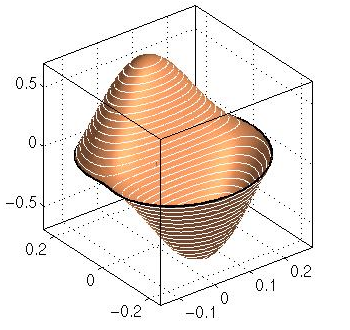 |
third eigenfunction, k2 = 286.0975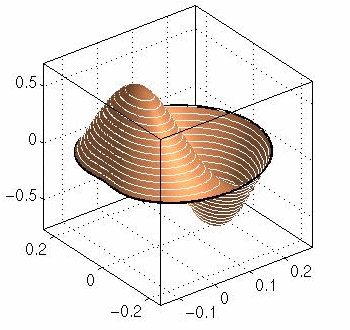 |
tenth eigenfunction, k2 = 960.0726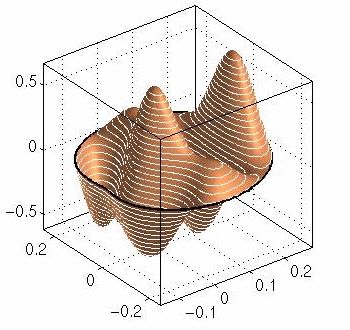
fiftieth eigenfunction, k2 = 4119.0409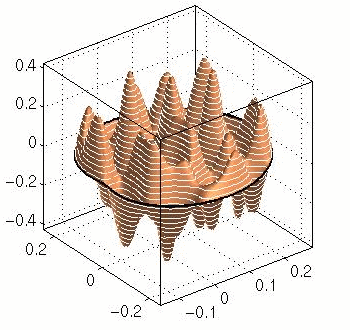
Literature
A. Richter: Playing Billiards with Microwaves - Quantum Manifestations of Classical Chaos, The IMA Volumes in Mathematics and its Application, Vol. 109, Springer 1999.See Publications for a complete list of WEB-publications.
Author: Bernhard Mößner ; Last modification: 2003/10/17 16:17:04 UTC.
| [Home] [The WEB-Method] [Examples] [Publications] [Contact] |