
| Home |
| The WEB-Method |
| Examples |
| Publications |
| Contact |
Multigrid Methods
Since there exists a simple subdivision scheme for b-splines, web-splines are ideally suited for multigrid techniques. A sequence of nested grids of width h, 2h, 4h, ... is used to reduce the residual error of the approximated solution and accelerate the iterative solution of the Galerkin system.
As a model problem, we consider Poisson's equation -div(grad(u))=1 with homogeneous Dirichlet boundary conditions on the following domain (left). The affiliated solution u is depicted on the right.
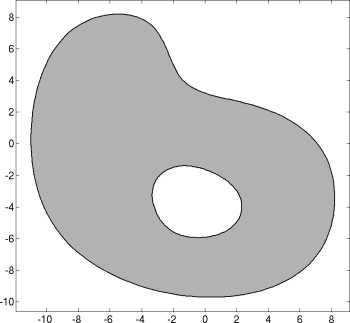 |
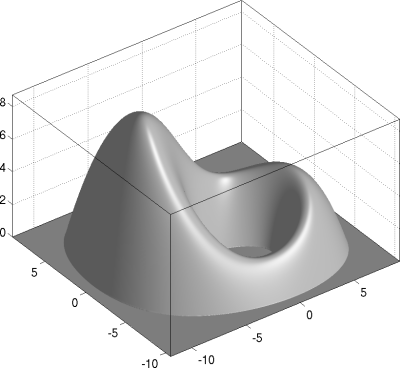 |
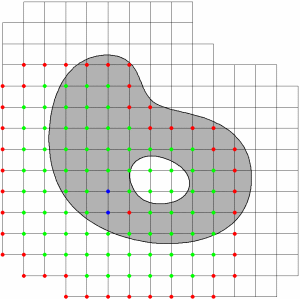
B-splines of degree 2 have been used on the following grids of width h=0.5, 1, and 2. Outer b-splines are marked red, extended b-splines green, and unextended b-splines blue.
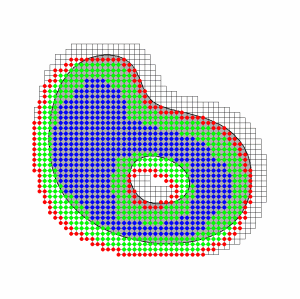 | 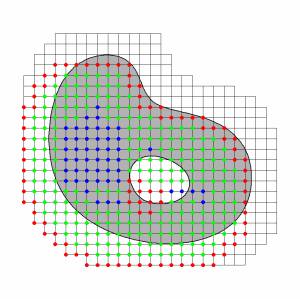 |  |
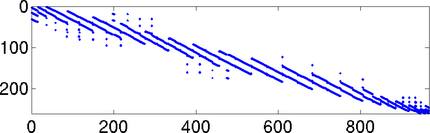
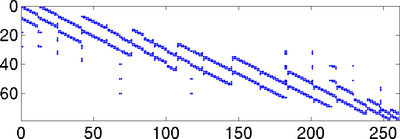
Grid transfer of correction vectors between the three web-spaces of dimension 966, 260, and 78 can efficiently be performed with the aid of sparse projection matrices with the following sparsity pattern:
 |
 |
Results of the dynamic multigrid solver (dmg) and a standard ssor preconditioned conjugate gradient solver (pcg) to achieve a residual norm <1e-10 are compared in the following table:
| h | web-splines | pcg iter | pcg rate | dmg iter | dmg rate | pcg time/dmg time |
|---|---|---|---|---|---|---|
| 2-1 | 966 | 19 | 0.28 | 60.75 | 0.67 | 0.67 |
| 2-2 | 3696 | 32 | 0.48 | 32.31 | 0.49 | 1.89 |
| 2-3 | 14383 | 61 | 0.68 | 29.31 | 0.45 | 3.72 |
| 2-4 | 56793 | 120 | 0.82 | 24.33 | 0.38 | 8.70 |
| 2-5 | 225593 | 239 | 0.91 | 22.33 | 0.36 | 19.40 |
| 2-6 | 899281 | 476 | 0.95 | 20.33 | 0.32 | 41.76 |
Each row represents one complete test using all grids of width 2-n,2-n+1,...,2 in case of the dmg solver, respectively one grid of width 2-n in case of the pcg solver. The second column lists the number of basis functions for the given grid width. Where pcg iter represents the number of pcg iterations, dmg iter represents the weighted number of ssor smoothing steps. A smoothing step on the finest grid of width h is weighted by 1, on the grid of width 2h by 1/4 and so on. The rate is computed by the iter-th root of the last residual norm. Since dmg smoothing steps are less expensive than pcg steps, the rates are not directly comparable. This is reflected by the ratio of solver times, which shows the immense speed-up by using the dynamic multigrid solver.
Literature
K. Höllig, U. Reif, J. Wipper: Multigrid methods with web-splines. Numerische Mathematik, Volume 91, Number 2, pp. 237-256, 2002.See Publications for a complete list of WEB-publications.
Author: Joachim Wipper ; Last modification: 2006/08/31 09:38:06 UTC.
| [Home] [The WEB-Method] [Examples] [Publications] [Contact] |