
| Home |
| The WEB-Method |
| Examples |
| Publications |
| Contact |
B-Splines and Tensor Product B-Splines
B-splines are fundamental to almost any application in geometric modeling. In particular, non-uniform rational B-spline representations (NURBS) have become a standard in CAD and CAM. Via the WEB-method, B-splines also provide very efficient finite element approximations.
B-splines are piecewise polynomial functions, which can be defined by a simple recursion. The following Figure shows B-splines of order 2 to 4 (piecewise polynomial functions of degree 1 to 3) on a uniform partition.

A B-spline of order n is positive and has compact support (marked red in the above Figure), consisting of n grid intervals. At the break points, the polynomial segments join with maximal smoothness, i.e., all but the (n-1)st derivative match.
Multivariate basis functions are constructed by multiplying B-splines corresponding to the different coordinates.
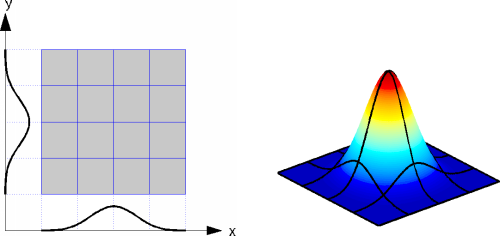
These so-called tensor product B-splines of order n also have compact support and are (n-2)-times continuously differentiable.
B-splines have the local approximation power of polynomials. Hence, high accuracy can be achieved already with relatively few basis functions.
Author: Joachim Wipper ; Last modification: 2006/08/31 09:38:46 UTC.
| [Home] [The WEB-Method] [Examples] [Publications] [Contact] |