
| Home |
| The WEB-Method |
| Examples |
| Publications |
| Contact |
Weight Function
In general, homogeneous boundary conditions cannot be modeled with tensor product B-splines. Therefore, we multiply the extended B-spline by a weight function, which is positive in the interior of the domain and vanishes on the boundary. The resulting weighted extended B-splines (WEB-splines) conform to homogeneous boundary conditions.
In the following we drescribe, by way of example, several techniques for constructing weight functions. To this end we consider a planar domain bounded by an ellipse and a circle, as depicted below.
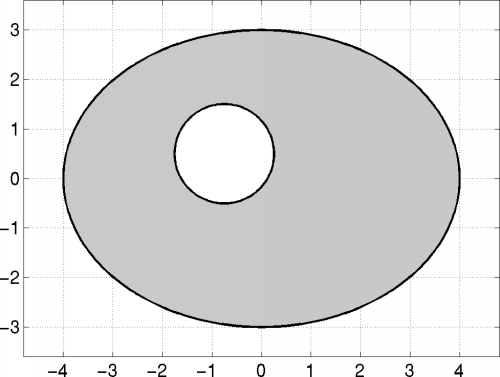
The boundary is represented in implicit form, i.e., with the following two functions.
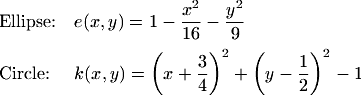
The function e(x,y) vanishes on the ellipse, and k(x,y) is zero only on the circle
Analytic Weight Function
Many elementary domains permit adhoc definitions of weight functions. For the example, the product of e and k is an obvious choice.
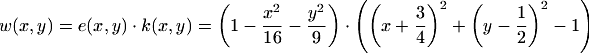
The Figure below shows this weight function on the domain, where it is strictly positive. If, as in this example, the weight function is globally defined and negative outside the domain, it can be conveniently used for in/out tests.
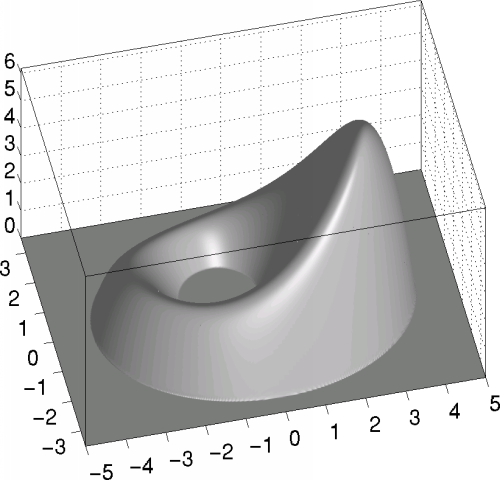
The construction of analytic weight functions is possible only for rather special domains, which include, however, many cases of practical interest.
Smooth Distance Function
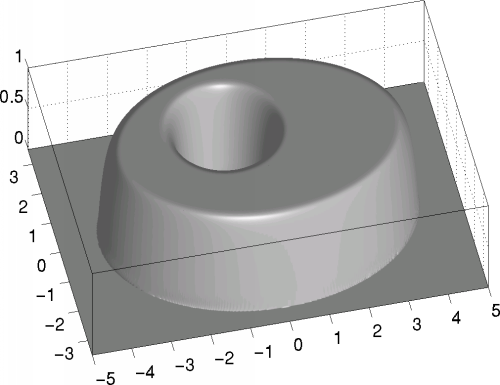
The distance function is used near the boundary, where it is free of singularities. Towards the interior of the domain it is blended with a plateau of height 1.
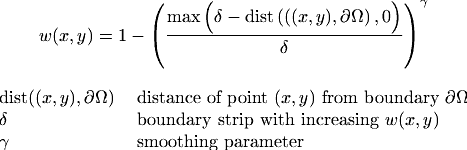
The width of the boundary strip depends on the smoothness of the distance function. In the following example it is set to 0.7.
R-Functions
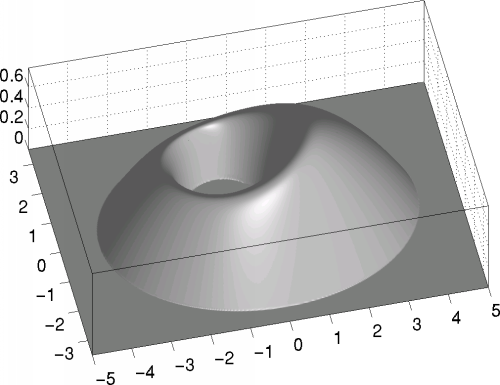
The R-function method of V.L. Rvachev allows to combine weight functions of different boundary parts yielding an algorithmic description of a global weight function. For the example,
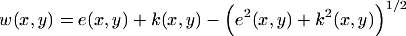
is obtained, which is shown below.
Integral representation of a weight function
The weight function
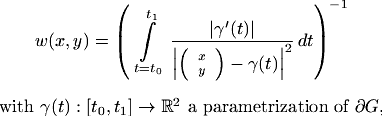
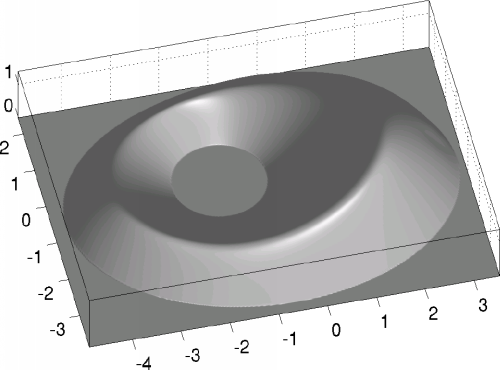
is proportional to the distance function and as smooth as the boundary of the simulation region G. On the entire boundary, the normal derivative equals 1/Pi. The following Figure shows this weight function for the domain defined above.
Author: Winfried Geis, Joachim Wipper ; Last modification: 2006/08/31 09:39:18 UTC.
| [Home] [The WEB-Method] [Examples] [Publications] [Contact] |