
| Home |
| The WEB-Method |
| Examples |
| Publications |
| Contact |
Error Estimates
To illustrate the WEB-method in an elementary setting, we consider a simple model problem, which has an analytic solution and, thus, permits the computation of exact approximation errors.
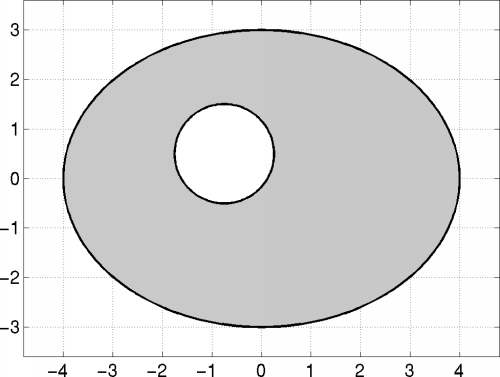
The simulation domain, shown above, is bounded by an ellipse and a circle.
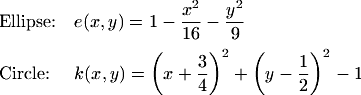
Numerical solutions are computed for Poisson's equation with homogeneous Dirichlet boundary conditions.
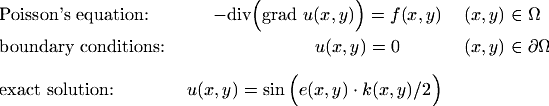
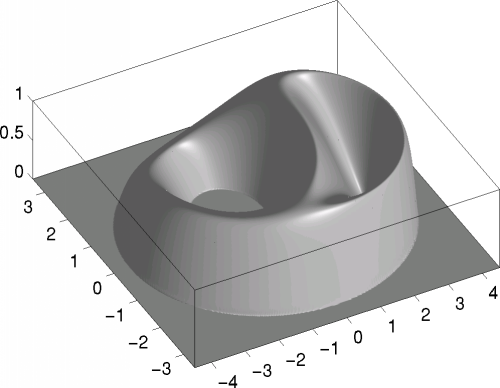
The right-hand side is chosen from a given exact solution, which is depicted below.
For the construction of the WEB-basis we used the analytic weight function
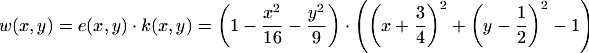
The error was measured in the following two norms.
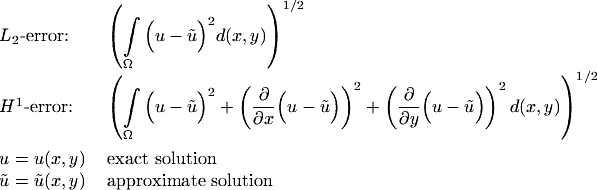
For B-splines of order 2 to 6 (polynomial degree 1 to 5)
the grid width was succesively halfed and the Ritz-Galerkin approximations computed. In the following diagram the L2-error was plotted versus the number of basis functions.
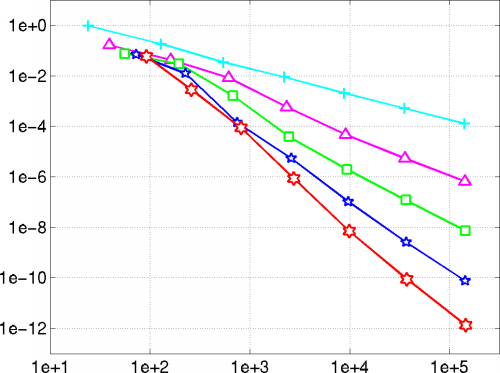
Dividing consecutive errors for a fixed order and taking logarithms with respect to the base 2 yields estimates for the convergence rate. The diagram below confirms that the optimal rates are attained.
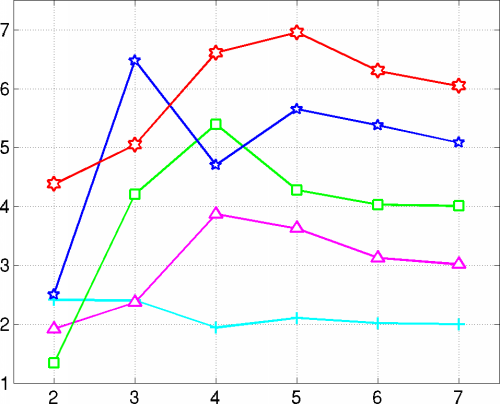
The H1-norm corresponds to the natural energy norm associated with Poisson's operator.
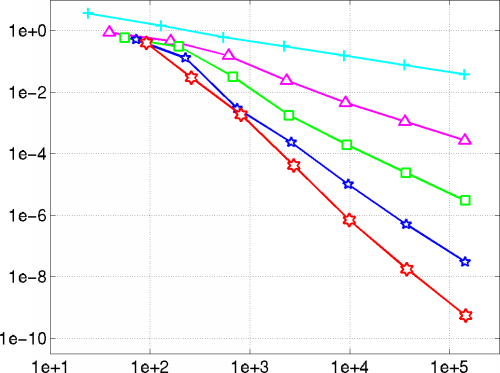
The optimal approximation order is equal to the degree of the WEB-splines (order minus 1). Again, the numerical results correspond to the theoretical predictions. The qualitative behavior of the error is similar as for the L2-norm.
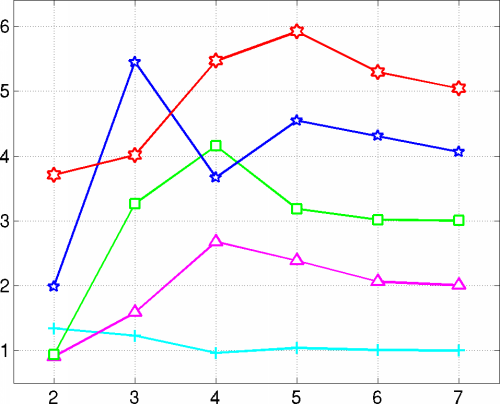
The following diagram compares the L2-error for WEB-splines to that of linear trial functions on a triangulation (black caro markers).
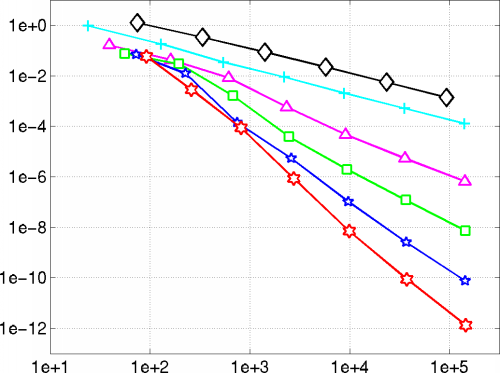
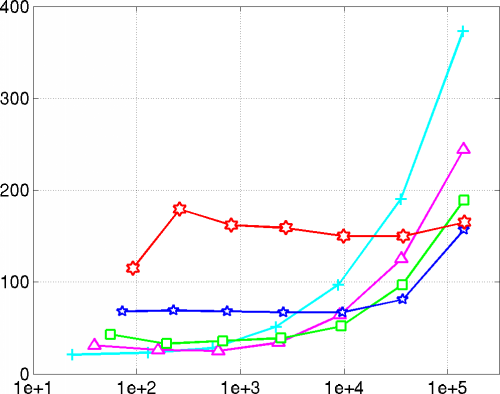
Because of the stabilization of the B-splines, the Ritz-Galerkin system can be solved efficiently with standard iterative methods, such as the preconditioned conjugate gradient algorithm. The following diagram shows the number of pcg-iterations for a tolerance of 1e-14 as a function of the dimension of the system.
Literature
K. Höllig, U. Reif, J. Wipper: Weighted extended b-spline approximation of Dirichlet problems. SIAM Journal on Numerical Analysis, Volume 39, Number 2, pp. 442-462, 2001.See Publications for a complete list of WEB-publications.
Author: Joachim Wipper ; Last modification: 2006/08/31 09:36:15 UTC.
| [Home] [The WEB-Method] [Examples] [Publications] [Contact] |